‎

Numbers

Thursday at the library

It’s Thursday afternoon and the von der Surwitz siblings meet in their reserved study room at the main university library to go over Wednesday’s lecture and examples. After Wednesday’s class, they’re glad they and the other ItCS participants had met with Professor Chandra at the Novalis Tech Open House two weeks prior to the start of school and had gotten a heads-up on what was ahead, including her repository. As a result they all had gone down the minimal prerequisite rabbit holes and were more or less ready.

Ursula von der Surwitz has plugged in her laptop to the big monitor and is scrolling through Professor Chandra’s first substantive lecture on Wednesday of the first week of classes¹¹ This is also on her GitHub repository. .

⌜…
For most of us our first experience with the abstraction power of numbers begins when our parents teach us to hold up three fingers to show everyone we’re three years old. And so we were introduced to the idea of seeing an abstract numerical magnitude such as the number three as a mapping or connection of three fingers to three years of life.

Then at some point we learn what mathematician Eugenia Cheng²² See her popular layman’s book How To Bake \(\pi\;\). One interesting aspect of this book is her treatment of category theory, which is a superset of type theory, much of which is baked into Haskell. calls the “counting poem,” i.e., we learn how to count from one to ten, usually on our fingers. And about this time we learn to negotiate numerically, like when we said, I’ll give so many of these if you give me so many of that. But then begins formal school math, and each year math becomes progressively less interesting, less popular — to the point of being a hated subject. This in my opinion is due to the curriculum being based on conditioned learning, the when you see this, do this method … unfortunately.

But if you major in math in college you eventually start to see in the later years³³ In many places in the world the typical American college Freshman-Sophomore math sequence of calculus, diff-eqs, and linear algebra is completed at the college-prep level. For example, Germany and Switzerland have college freshmen starting with Analysis. — after the four Freshman and Sophomore semesters of calculus, differential equations, and linear algebra — what is commonly called “higher math.” And these upper-semester math courses can be a complete reboot of math, weeding out vague, ad hoc, parochial⁴⁴ parochial: … very limited or narrow in scope or outlook; provincial… notions, replacing them with a rigorous, theoretical, formalistic, foundational understanding of math. As mathematician Joe Fields says, this is when you stop being a “see this, do this” calculator and become a prover, i.e., a deeper thinker about math.

Set theory is a big part of this formalism⁵⁵ Make sure you’re attacking the LibreTexts series, e.g., one of the first three rabbit holes in the math section. . Set theory is an exacting, don’t-take-stuff-for-granted world, which turns out to be good for the computer world as well since computer circuits don’t attend human grade school, don’t learn poems, and don’t have fingers⁶⁶ If machines were capable of conditioned learning, your car should be able to self-drive certain oft-travelled routes, e.g., from your home to the grocery store. . Again, if you want a computer to understand something, you have to spell it out in very precise and exacting ways. That is to say, you’re always facing logical entailment (LE) with computers. So how then does a computer understand numbers? And isn’t a computer doing numbers the same way a clock does time? Think about it. Does a ticking clock that you have to wind up have any real concept of time? No, it doesn’t.

One fascinating twist of mathematical history is how, on the whole, the Greeks seemed to favor geometry over numbers. Their mastery of geometry really got going with Euclid’s Elements ca. 300 BC, which starts with just a point and a line and from there builds up expansive theorems about complex geometric shapes, i.e., no numbers⁷⁷ It was a long-revered feat of logical minimalism that all two-dimensional shapes in Elements could be produced with just a compass and a straightedge. Follow the Wikipedia link and note the animation of the construction of a hexagon. It wasn’t until the development of calculus and infinitesimal methods in the Renaissance that this compass-and-stick purity was set aside. . Even when Euclid’s geometry worked with the concepts of length and angles, no numbers were employed⁸⁸ Later we’ll explore how Descartes united algebra and geometry. . And as the physicist Julian Barbour said, A triangle is known for its shape not its size.

This week we’ll talk about numbers in a fairly theoretical but not really difficult manner. Along with the math, we’ll do some work with Haskell that you should be ready for⁹⁹ Make sure you’re getting along with the Haskell rabbit hole materials — at the very least worked through half of LYAHFFG. .
…⌟

𝔘𝔯𝔰𝔲𝔩𝔞: So like Professor Chandra said yesterday, we need to see things in terms of set theory from here on out.
[murmurs of agreement]
𝔘𝔴𝔢: And like she said, with set theory we can properly define relations and function. All of which sounds rather ominous. Like everything we thought we knew was about to go away.
[more agreement murmurs]
𝔘𝔯𝔰𝔲𝔩𝔞: [continuing] So here’s her breakdown of what she called number classification or taxonomy. [scrolling…]

⌜…

\(\mathbb{N}\;\): the natural counting numbers, often starting with \(0\;\); otherwise, with \(1\;\).
\(\mathbb{Z}\;\): whole number integers — just like \(\mathbb{N}\;\) but with the positive numbers duplicated as negative numbers, along with \(0\;\) between them.
\(\mathbb{Q}\;\): the rational numbers — composed as \(\frac{a}{b}\;\) where \(a\) and \(b\) are integers and \(b\) cannot be \(0\;\) — although this is really too simple and we’ll be expanding on it later.
\(\mathbb{R}\;\): the real numbers are the limit of a convergent sequence of rational numbers… Really? Yes, but this is a higher math sort of definition. Suffice it to say for now reals are the rational numbers (including recurring decimals) along with ir-rational numbers (non-recurring decimals), e.g., the square root of \(2\;\). In other words, numbers that are expressed with decimals¹⁰¹⁰ Two questions: Are repeating decimal numbers also rational? If yes, then why can’t rational numbers represent all numbers? That is, why do we need real and complex numbers? Programming challenge: Write a function that takes a real decimal number and figures out its fraction, e.g. \(3.14\) is \(157/50\:\). Does Haskell have a built-in way to do this? Hint: Check out Convert decimal number to rational. Maybe compare with how Julia and Racket do it. . Lots more to come…
\(\mathbb{C}\;\): the complex numbers are of the form \(a + bi\;\) where \(a\) and \(b\) are real numbers and \(i\) is the square root of \(-1\;\). Again, lots more later.

…⌟

𝔘𝔴𝔢: Right. We’re not supposed to worry about this too much yet; we’ll go into it more later. Just realize that we’re talking about the set of natural numbers, the set of real numbers, et cetera.
[murmurs of agreement]
𝔘𝔱𝔢: Their traits and properties, as she said. And the fact that each number “species” is a subset of the next one up [writing on the whiteboard]

\begin{align*} \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}\ \subset \mathbb{C} \end{align*}

𝔘𝔱𝔢: [continuing] One is contained by the other.
𝔘𝔴𝔢: [paging through his written notes] Then she once more drove home the point that set theory is important [quoting]

⌜…
Set theory is the basic foundation of math, and is fundamental to the discrete math of computer science. But there’s a new kid is on the block, namely, category theory, which is even more foundational than set theory. With Haskell we’ll encounter some of the rudiments of category theory now and then.
…⌟

𝔘𝔴𝔢: Anybody know what that means?
𝔘𝔯𝔰𝔲𝔩𝔞: We all watched the video? [clicking on this YouTube link] Did you all watch it?
𝔘𝔱𝔢: Ahhh, yes, but I can tell I’m a long way from really getting it, or why it’s such a big deal.
𝔘𝔴𝔢: So we see a bunch of stuff we supposedly already know being repackaged in a way that uncovers how we really only had a superficial understanding of the concepts.
[laughter]
𝔘𝔯𝔰𝔲𝔩𝔞: I watched it, but it’ll take some time to sink in because [nodding to Uwe] on one level I guess I understood, but I don’t think I caught what the whole point was¹¹¹¹ Professor Chandra connected this to Haskell by mentioning Haskell’s “point-free” programming … but didn’t elaborate. . I suppose that’s coming as well.
𝔘𝔱𝔢: But wasn’t it a bit ominous the way she said this is higher math — if not grad school stuff? But we’re not supposed to be intimidated! No! At least not yet.
[nods and laughter]
𝔘𝔴𝔢: Like they’ve been saying, we’re Versuchskaninchen.
[laughter]
𝔘𝔱𝔢: Guinea pigs. No, but I’m getting the impression this could be a great course.
[nods]

Numbers in Haskell

𝔘𝔯𝔰𝔲𝔩𝔞: [scrolling] So we then come to Haskell’s version of the numbers.
[all study the screen]
𝔘𝔱𝔢: Which is supposed to be close to the whole mathematical taxonomy.

⌜…

Int: limited-precision integers in at least the range \([-2^{29} , 2^{29})\;\).
Integer: arbitrary-precision integers (read lots of integers, lots more than Int).
Rational: arbitrary-precision rational numbers.
Float: single-precision floating-point numbers.
Double: double-precision floating-point numbers
Complex: complex numbers as defined in Data.Complex.

…⌟

𝔘𝔯𝔰𝔲𝔩𝔞: And she tells us not to worry about what precision and floating-point mean for the time being.
𝔘𝔱𝔢: Right, because they’re part of how the electrical logic circuits do numbers. The whole “logical entailment” of doing numbers on an electric machine thing.
[murmurs of agreement]
𝔘𝔴𝔢: And we’re not to worry about natural numbers yet. We’ll do those separate.
[murmurs of agreement]

The qualities of quantity

𝔘𝔯𝔰𝔲𝔩𝔞: [scrolling] So here’s more.

⌜…
A number is a concept, first and foremost a symbol related to quantity and magnitude. And as such a number has great powers of abstraction. Numbers may be applied in the abstraction exercises of counting or enumerating, as well as measuring things¹²¹² But then measuring must be “quantified” by counting unit-wise what was measured; hence, everything comes back to counting. This will come up when we explore real numbers versus rational numbers. .

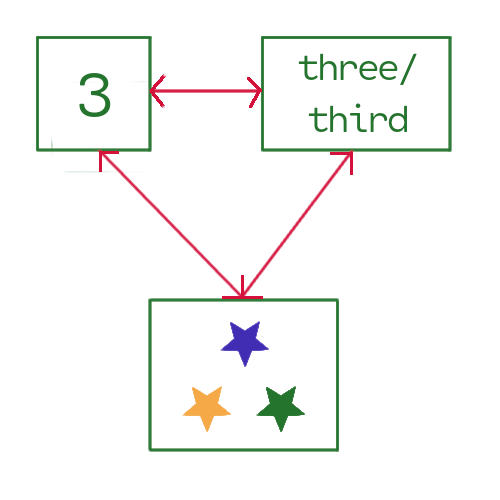The concept, the embodiment of three and "three-ness"

Consider these qualities of quantities

cardinality, or how many?
ordinality, or what order?
enumeration, or, generally, how do we count out things?

As we’ve said, when we bring the computer into this quantification game, we cannot assume these basic qualities as given¹³¹³ Inside your head you automatically know how many and in what order the numbers \(1\) through \(10\) are. However, a computer must be taught such basic quantitative qualities. .
…⌟

𝔘𝔯𝔰𝔲𝔩𝔞: [continuing] Any thoughts, questions?
[all study the screen]
𝔘𝔱𝔢: Let’s go on.

Cardinality

⌜…
In everyday language cardinal numbers are simply the counting numbers, \(\mathbb{N}\;\), either as words or numerical symbols. In set theory, however, cardinality has a different meaning, i.e., the number the objects in a set. So if we consider the box of stars in the diagram above to be a set of stars, then the cardinality of this set is \(3\) since there are three stars¹⁴¹⁴ We indicate the set’s cardinality by surrounding the symbol for a set with pipes ( | ), e.g., \(|S_{stars}|\;\). This is not the same as absolute value, although they might be cousins.

\begin{align*} |\,S_{stars} \,| &= 3 \\ |\,\{a, b, c\}\,| &= 3 \\ |\,\mathbb{N}\,| &= \infty \\ |\,\mathbb{Z}\,| &= \infty \end{align*}

But why are we being so “conceptual” about the simple idea of amount, and why must we give it a fancy name? Again, math likes to formalize things, nail things down. Starting with exactness and precision we can then build very complex and logically-based math¹⁵¹⁵ Have a look at this Wikipedia discussion of cardinality. Later we will look into cardinal numbers, which is a deeper dive into set theory. . Now, if two sets have the same cardinality, is this somehow significant? Above, we see that both the set of natural numbers and the set of integers have infinity as their cardinality. Are, therefore, \(\mathbb{N}\) and \(\mathbb{Z}\) the same “size?”

The bijection principle states that two sets have the same size if and only if there is a bijection (injective and surjective together) between them¹⁶¹⁶ We’ll look at injective, surjective, and bijective when we delve into functions from a set theory perspective. Also, mathematical logic will introduce us to if and only if. .

Which means \(|\,S_{stars} \,|\;\) and \(|\,\{a, b, c\}\,|\;\) can be matched up one-to-one, thus, they must have the same cardinality. But again, what about sets of things that supposedly have an infinite size? How do we “count,” or “pair up” infinite sets¹⁷¹⁷ To excite your curiosity, isn’t \(\infty + 1\) still just \(\infty\;\)? The Greeks contemplated this and concluded that infinity has the power to consume, destroy individual numbers. It wasn’t until the German mathematician Georg Cantor came along in the late nineteenth century that we learned to wrangle infinity. ? Surprisingly, there are different kinds of infinity — which necessitates this exactness and preciseness. More about cardinality theory later.
…⌟

𝔘𝔴𝔢: So basically, cardinality is a formalism from set theory about amount and magnatude. Fair enough.
𝔘𝔯𝔰𝔲𝔩𝔞: What about this section? [scrolling]

Haskell and cardinality

⌜…
The first thing to know about Haskell and set theory is, yes, we can do real set theory with Haskell’s Data.Set package. But as beginners learning the ropes we will start with a simpler representation of sets through Haskell’s basic list data structure. Realize, however, that a list is not a set; they are two different beasts, and we’ll have to account for that. For one, a set may have duplicates, whereas a list holds a definite sequence of things, i.e., every element of the list is unique, even if some elements are repeated¹⁸¹⁸ So it’s not really a “grocery list,” it’s a “grocery set” since \(\{eggs,sugar,coffee,eggs\}\;\;\;\) is invariably interpreted as just \(\{eggs,sugar,coffee\}\;\;\), right? Or would you go ahead and get eggs twice? Can you come up with another real-world example where a set of things doesn’t care about order or duplicates? . So the set \(\{1,2,1\}\;\) is the same as \(\{1,2\}\;\) is the same as \(\{2,1,1\}\;\) because sets don’t mind duplicates, nor do they worry about order¹⁹¹⁹ Why is this? There is a LE to the definition of a set union, namely, \(A \cup B = \{x \;\;|\;\; x \in A \;\;\;or\;\;\; x \in B \}\quad\). Consider the sets \(A = \{1,2,3\}\;\), \(B = \{2,3,4\}\;\), and \(C = \{3,4,5\}\;\). If you draw out Their union \(A \cup B \cup C = \{x \;|\; x \in A \;\;\text{or}\;\;x \in B\;\; \text{or}\;\;x \in C \}\quad\;\;\) as a Venn diagram, you’ll see how duplicates get left out. . But the lists [1,2,1], [1,2], and [2,1,1] are in fact all different lists. Initially, we’ll practice set theory with lists and build alternate set theory code based on lists. Then when we understand “squirrel math” a little more, i.e., how to work with the data structures known as trees, we’ll do proper set theory with Haskell’s set theory module, Data.Set²⁰²⁰ Take a look at this Hackage page. It has an intro to Haskell’s sets. Get in the habit of perusing Hackage whenever you’re using a Haskell function or data type you don’t quite understand. Sometimes you’ll have to just dive into the code, but sometimes there are excellent intro docs like this. And yet there are also set operations in Data.List. Perhaps look into these two options. . For the immediate future we’ll consider a list to be a beginner’s substitute for a set. And so a simple “how many” function on a list standing in for a set is length. The code

length [1,2,3,4,5]

<interactive>:322:9: warning: [-Wtype-defaults]
    • Defaulting the type variable ‘a0’ to type ‘Integer’ in the following constraint
        Num a0 arising from the literal ‘1’
    • In the expression: 1
      In the first argument of ‘length’, namely ‘[1, 2, 3, 4, ....]’
      In the expression: length [1, 2, 3, 4, ....]

<interactive>:322:9: warning: [-Wtype-defaults]
    • Defaulting the type variable ‘a0’ to type ‘Integer’ in the following constraint
        Num a0 arising from the literal ‘1’
    • In the expression: 1
      In the first argument of ‘length’, namely ‘[1, 2, 3, 4, ....]’
      In the expression: length [1, 2, 3, 4, ....]
5

Again, more to come. Watch this space²¹²¹ Meanwhile, here’s a brain-teaser that goes to the heart of this set-list issue — especially in Haskell, Why are set union and intersection commutative and associative due to their lack of order? .
…⌟

𝔘𝔴𝔢: So, bottom line, we’re not going to have real sets with Haskell right away, just a sort of Ersatz sets with lists. Are we all sort of familiar with Haskell lists from the Learn You…?
[murmurs of affirmation as Ursula clicks on a tab showing LYAHFGG’s section on lists]
𝔘𝔱𝔢: So what about finding another example of sets having duplicates and being in different order? [looks back and forth]
𝔘𝔯𝔰𝔲𝔩𝔞: Well, here’s mine [scrolling to her personal annotation of the professors notes and reading aloud]

⌜…
A “set” of students in a class pass around a sign-in sheet each day on which they sign their name. Some days the names are in one order, other days another order, depending on how it was passed around the room. And sometimes a student accidentally signs twice. But it’s still the same set of students, order and duplicate sign-ins notwithstanding.
…⌟

𝔘𝔴𝔢: Oooh, notwithstanding! You’re getting fancy with your English.
[laughter]
𝔘𝔯𝔰𝔲𝔩𝔞: Hey, no brain-shaming!
[laughter]
𝔘𝔴𝔢: [continuing] No, really, that’s a great example because it brings out the difference between the actual set and how it’s being — represented.
𝔘𝔱𝔢: So do we all understand her side note about set unions?
𝔘𝔴𝔢: I drew some Venn diagrams [pulls out a hand drawing and places it on the table] and, yes, you can see how all the overlaps are telling us not to worry about the duplicates of the individual sets making up the union.
𝔘𝔱𝔢: Right, and it’s curious how when you just look at the set notations, you don’t necessarily see that. At least I don’t. I mean [writing on the board] \(A \cup B \cup C = \{x \;|\; x \in A \;\;\text{or}\;\;x \in B\;\; \text{or}\;\;x \in C \}\quad\;\;\) doesn’t necessarily tell you it doesn’t want duplicates.
𝔘𝔴𝔢: By the way, don’t forget union and intersection are binary, right?
[nods of agreement]
𝔘𝔱𝔢: All right then, [correcting her formula] \(A \cup B = \{x \;|\; x \in A \;\;\text{or}\;\;x \in B\;\}\;\;\;\;\). Satisfied?
[Ursula giggles]
𝔘𝔴𝔢: All right, unless you have the word or to mean that we don’t keep picking up the same element from the different sets. But the inclusive or of set union means it can be from one or the other — or from both of them. So I definitely see your point, the set notation doesn’t tell us not to include duplicates — without some exclusive sort of inclusive or. Only the Venn diagram really shows us this. I mean, the whole point of this is to think about whether the definition of set union rules out duplicates, doesn’t worry about order, and has commutativity. I don’t see that
[murmurs of agreement]
𝔘𝔱𝔢: So in the rabbit hole on logic, we had the truth tables, right? So they talked about logical or, which they also called disjunction. And then they had a truth table for or which showed how the only time something wasn’t true was when both of the statements were false.
𝔘𝔴𝔢: Basically, it’s the same operations with both sets and logic.
𝔘𝔯𝔰𝔲𝔩𝔞: More later.
[murmurs of agreement]
𝔘𝔯𝔰𝔲𝔩𝔞: All right, so what about this brain teaser?
𝔘𝔱𝔢: Right. [getting up and writing on the board]

\begin{align*} A \cup B &= B \cup A, \\[.5em] A \cap B &= B \cap A, \\[.5em] (A \cup B) \cup C &= A \cup (B \cup C), \quad and \\[.5em] (A \cap B) \cap C &= A \cap (B \cap C) \end{align*}

𝔘𝔱𝔢: [continuing] The first thing we have to know is what are union and intersection in the world of lists? I figured out that putting lists together come in two forms, the cons operation, and the concatenation operator.
𝔘𝔯𝔰𝔲𝔩𝔞: Right. Like this. [creating a source block]

1 : []

<interactive>:324:1-6: warning: [-Wtype-defaults]
    • Defaulting the type variable ‘a0’ to type ‘Integer’ in the following constraints
        (Show a0) arising from a use of ‘print’ at <interactive>:324:1-6
        (Num a0) arising from a use of ‘it’ at <interactive>:324:1-6
    • In a stmt of an interactive GHCi command: print it
[1]

𝔘𝔯𝔰𝔲𝔩𝔞: [continuing] for cons and then this for concatenation

[1] ++ [2]

<interactive>:326:1-10: warning: [-Wtype-defaults]
    • Defaulting the type variable ‘a0’ to type ‘Integer’ in the following constraints
        (Show a0) arising from a use of ‘print’ at <interactive>:326:1-10
        (Num a0) arising from a use of ‘it’ at <interactive>:326:1-10
    • In a stmt of an interactive GHCi command: print it
[1,2]

𝔘𝔴𝔢: You showed me that stackoverflow post where they created a union function for lists. But then one commentor noted how no, these list versions of union didn’t allow for commutativity and all.
𝔘𝔯𝔰𝔲𝔩𝔞: Exactly. Only the Data.Set, the true set theory package did.
[silence while digesting the ideas]
𝔘𝔱𝔢: Yeah, right, I looked through it, but I consider myself just a beginner with Haskell, but it seemed to be talking mainly about how you eliminate duplicates.
𝔘𝔴𝔢: But what about that “equational reasoning”? One of you guys went into that, didn’t you?
[Ursula and Ute trade glances]
𝔘𝔱𝔢: Well, I looked it up on Wikipedia and was redirected to an article that was actually called Universal algebra [Ursula brings up the article on the monitor], and in the Basic idea section
𝔘𝔴𝔢: Once again, on that fateful day when we sat down and talked with Professor Chandra she told us to not fear the rabbit hole!
[laughter]
𝔘𝔱𝔢: And to expect a whole new way of seeing math.
𝔘𝔴𝔢: Right, that didn’t present itself serially, one thing after another. No, we’re taking this on in parallel.
[murmurs of agreement]
𝔘𝔱𝔢: I did email Professor Chandra, and she said the Universal algebra page was not very specific for what Haskell meant by equational reasoning — and she gave me another link, which we can look at — but that it contained a lot of good stuff, and we should try to get the gist of it.
[rueful murmurs]
𝔘𝔱𝔢: [continuing, reading from her laptop]

⌜…
An algebraic structure consists of a nonempty set \(A\) (called the underlying set, carrier set or domain), a collection of operations on \(A\) (typically binary operations such as addition and multiplication), and a finite set of identities, known as axioms, that these operations must satisfy.
…⌟

𝔘𝔯𝔰𝔲𝔩𝔞: [bringing the page up on the monitor] Here it is.

import Data.Set (Set, lookupMin, lookupMax)
import qualified Data.Set as Set

Set.union (Set.fromList [1, 3, 5, 7]) (Set.fromList [0, 2, 4, 6])

<interactive>:328:1-9: error:
    Not in scope: ‘Set.union’
    NB: no module named ‘Set’ is imported.

<interactive>:328:12-23: error:
    Not in scope: ‘Set.fromList’
    NB: no module named ‘Set’ is imported.

<interactive>:328:40-51: error:
    Not in scope: ‘Set.fromList’
    NB: no module named ‘Set’ is imported.

Set.union (Set.fromList [0, 2, 4, 6]) (Set.fromList [1, 3, 5, 7])

<interactive>:330:1-9: error:
    Not in scope: ‘Set.union’
    NB: no module named ‘Set’ is imported.

<interactive>:330:12-23: error:
    Not in scope: ‘Set.fromList’
    NB: no module named ‘Set’ is imported.

<interactive>:330:40-51: error:
    Not in scope: ‘Set.fromList’
    NB: no module named ‘Set’ is imported.

Set.empty

’
    NB: no module named ‘Set’ is imported.

Set.union (fromList [1,2,3]) (Set.empty)

<interactive>:334:1-9: error:
    Not in scope: ‘Set.union’
    NB: no module named ‘Set’ is imported.

<interactive>:334:31-39: error:
    Not in scope: ‘Set.empty’
    NB: no module named ‘Set’ is imported.

Set.intersection  (fromList [1,2,3]) (Set.empty)

<interactive>:336:1-16: error:
    Not in scope: ‘Set.intersection’
    NB: no module named ‘Set’ is imported.

<interactive>:336:39-47: error:
    Not in scope: ‘Set.empty’
    NB: no module named ‘Set’ is imported.

import Data.Ratio

𝔘𝔯𝔰𝔲𝔩𝔞: Let’s leave it for now. So moving on [scrolling].

Numbers

Thursday at the library

Numbers in Haskell

The qualities of quantity

Cardinality

Haskell and cardinality

Ordinality

Ordinality in Haskell

Types of types

The `Num` super class

GHC.Num

Numbers

Thursday at the library

Numbers in Haskell

The qualities of quantity

Cardinality

Haskell and cardinality

Ordinality

Ordinality in Haskell

Types of types

The Num super class

GHC.Num

The `Num` super class